Jak se skládá kvádr?

Jak se pocita kvádr

U kvádru můžou být všechny tři rozměry různé (délka, šířka a výška), proto těmto rozměrům obecně přiřazujeme tři různá písmenka – „a, b, c“. Objem kvádru vypočítáme tak, že spočteme obsah podstavy (obdélník – S=a.b), kterou dále vynásobíme výškou kvádru (c). Výsledná hodnota je v objemových jednotkách.
Archiv

Jak se vypočítá obsah kvádru

Obsah kvádru se počítá jako délka hrany [a] x délka hrany [b] x délka hrany [c].

Jak se rýsuje síť kvádru

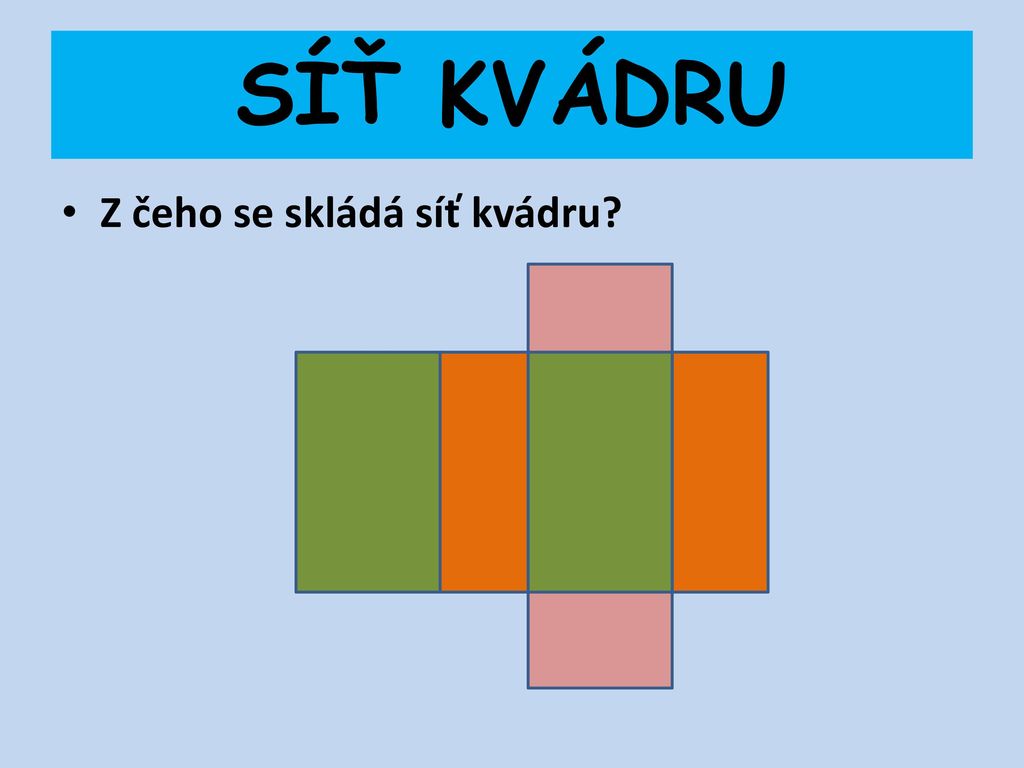
Rozložíme – li kvádr na jednotlivé shodné obdélníky (v některých případech na obdélníky a čtverce), získáme SÍŤ KVÁDRU. Spočítej, z kolika STĚN se skládá síť krychle Vedle sítě kvádru je znázorněn samotný kvádr. Všimni si jeho zvýrazněných částí – nazýváme je HRANY.
ArchivPodobné

Co je podstava kvádru

Kvádr je prostorové těleso, jehož podstavou je čtverec nebo obdélník a boční stěny jsou kolmé na podstavu. Dvě protější stěny jsou stejné. Kvádr má osm vrcholů, dvanáct hran, šest stěn, dvanáct stěnových úhlopříček, čtyři tělesové úhlopříčky.
Archiv

Jak se vypočítá obvod kvádru

Vzorce pro výpočet kvádruObvod: O = 4 (a + b + c)Plocha jedné strany: P = a × b nebo b × c nebo a × c.Celková plocha: Q = 2 (ab + bc + ac)Objem: V = a × b × c.Úhlopříčka stranová: u2 =Úhlopříčka tělesová: u3 = √(a2 + b2 + c2)

Co má tvar kvádru

tvar koule – míč, kulový kryt lampy, tvar kvádru – krabička od sirek, panelový dům s vodorovnou střechou, tvar válce – hrneček. Je důležité, aby si žáci uvědomili, že i třída, různé místnosti mají v podstatě tvar kvádru, pokud pomineme různé výklenky a otvory oken a dveří.

Jak vypadá krychle

Krychle (pravidelný šestistěn nebo také hexaedr) lidově zvaná též kostka, je trojrozměrné těleso, jehož stěny tvoří 6 stejných čtverců. Má 8 rohů a 12 hran. Patří mezi mnohostěny, speciálně mezi takzvaná platónská tělesa.

Jak se kreslí krychle

1) narýsujeme si přední stěnu, je to krychle, takže všechny stěny tvoří čtverce, zvolíme a = 4 cm. 2) u každého vrcholu čtverce si uděláme pomocnou polopřímku pod úhlem 45°. Dáme si do kružítka polovinu strany čtverce (tedy 2 cm) a na každou polopřímku si narýsujeme oblouk. Vzniknou nám 4 další vrcholy krychle.

Jaký je rozdíl mezi hranolem a kvádrem

KVÁDR. Za kvádr považujeme kolmý hranol, jehož podstavou je obdélník nebo čtverec. Tudíž se jedná o čtyřboký hranol. V případě, že podstavy kvádru jsou čtverce, jedná se o pravidelný čtyřboký hranol.

Jak vypadá kvádr

Kvádr má šest stěn obdélníkového tvaru (ve speciálních případech 2 čtvercové + 4 obdélníkové nebo 6 čtvercových) z nichž dvě protilehlé jsou vždy shodné, osm vrcholů a dvanáct hran z nichž čtveřice rovnoběžných má vždy shodnou délku.

Jaký je vzorec pro výpočet povrchu kvádru

KVÁDRZa kvádr považujeme kolmý hranol, jehož podstavou je obdélník nebo čtverec.Objem V kvádru o rozměrech a b c je.V =abc.Povrch S kvádru o rozměrech a b c je.S =2ab+2(ac+bc)=2(ab+ac+bc).Krychle je speciální případ kvádru, jehož rozměry se rovnají (a=b=c); nebo-li výška krychle je rovna délce podstavné hrany.

Jaký je rozdíl mezi krychli a kvádrem

Krychle je geometrické těleso, které má tři rozměry. Skládá se ze šesti navzájem shodných čtverců. Kvádr je geometrické těleso, které má tři rozměry. Skládá se ze šesti obdélníků, přičemž každé dva obdélníky, které jsou proti sobě jsou shodné.

Jak se počítá povrch krychle

Vzorce pro výpočet povrchu krychle

Obsah jedné stěny tj. jednoho čtverce vypočítáme jednoduše podle vzorce [S] = a × a. Výsledek následně vynásobíme šesti a tak získáme povrch krychle. Zjednodušení výpočtového vzorce: [S] = 6 × a × a => 6 × a2.

Co to je krychle

Jak se počítá obvod kvádru

Jak se značí povrch kvádru

Stěny kvádru jsou obdélníky, přičemž vždy dvě jsou stejně velké. Povrch tedy vypočítáme jako S = 2 ( a b + a c + b c ) S = 2(ab+ac+bc) S=2(ab+ac+bc).

Jaký je vzorec pro povrch kvádru

Jak zjistit povrch kvádru

Plocha tělesa je součet obsahů všech stěn (nebo spíš jejich povrchů) na prostorových objektech. Kvádr má 6 obdélníkový stěn. Pokud chceme najít povrch kvádru, můžeme sečíst všech 6 stěn. Nebo můžeme označit délku (l), šířku (š) a výšku (h) hranolu a k vypočítání plochy použít vzorec: S=2lš+2lh+2hš.

Jak spočítat obvod kvádru