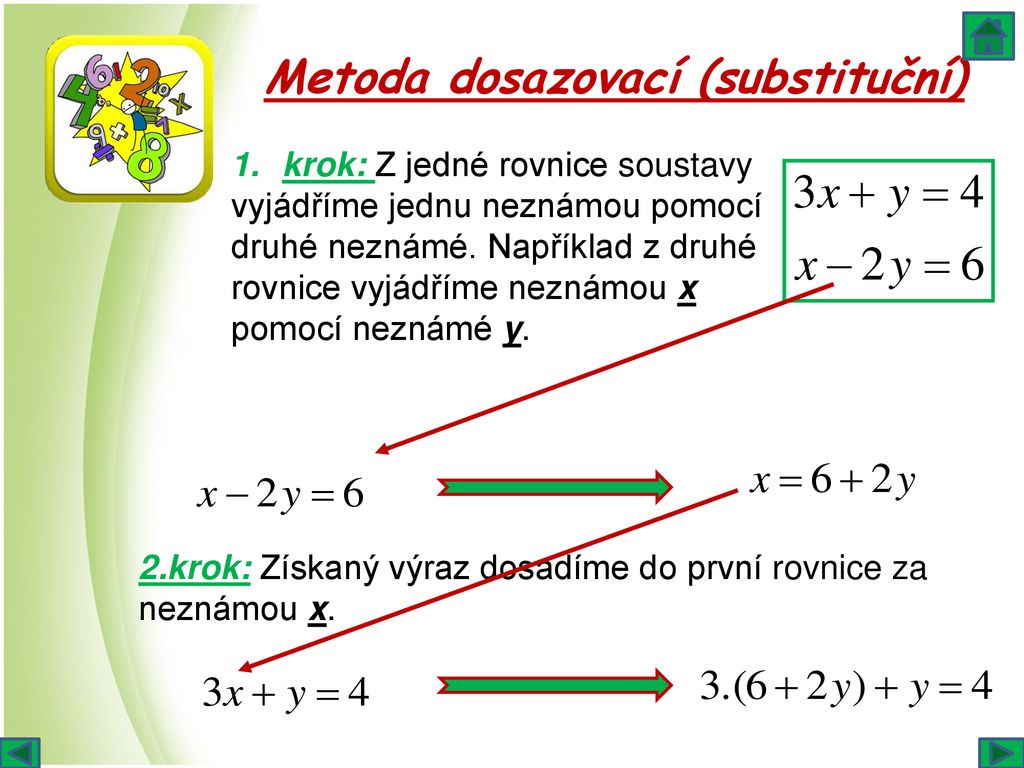
Jak se dělá Dosazovaci metoda?

Jak se pocita sčítací metoda

Sčítací metoda

Při řešení sčítací metodou sečteme (či odečteme) odděleně levé a pravé strany obou rovnic. Tato úprava vede k cíli, pokud nám při této operaci jedna z proměnných vypadne. V některých případech je proto nutné nejdříve jednu z rovnic vynásobit vhodným číslem.
Archiv

Jak počítat s dvěma neznámými

Rovnice o dvou neznámých řešíš tak,že musíš vypočítat ze zadané rovnice první neznámou tedy x a tu dosadit do druhé rovnice a vypočítat z ní druhou neznámou tedy Y a tu dosadit do první rovnice a vypočítat číselnou hodnotu první neznámé tedy x.Je to metoda substituční,druhá metoda je sčítací a násobná,tím,že obě …

Jak se dělá zkouška u rovnic

Zkouška – kontrola správnosti dosazením nalezeného kořene do obou stran původní rovnice. Ekvivalentní úpravy rovnic (nezmění kořeny původní rovnice) – Přičtení (odečtení) stejného čísla nebo mnohočlenu k oběma stranám rovnice. – Vynásobení (vydělení) obou stran rovnice stejným nenulovým číslem.
ArchivPodobné

Jak se počítají soustavy rovnic

Když řešíme soustavu rovnic dosazovací metodou, musíme udělat následující:Osamostatnit v jedné z rovnic jednu z neznámých, např. rovnici 2x+y=3 napíšeme jako y=3-2x.Takto osamostatněnou neznámou už máme vyjádřenou pomocí druhé neznámé. Dosadíme tento výraz do druhé rovnice, např.Teď už máme rovnici s jednou neznámou!

Kdy má rovnice nekonečně mnoho řešení

Soustava lineárních rovnic nemá žádné řešení tehdy, když jsou grafy jednotlivých rovnic navzájem rovnoběžné. Nekonečně mnoho řešení. Soustava lineárních rovnic má nekonečně mnoho řešení tehdy, když grafy jednotlivých rovnic tvoří tu samou přímku.

Jak řešit 3 rovnice o třech neznámých

Soustavu vyřešíme dosazovací metodou (můžeme si vybrat také sčítací nebo srovnávací metodu). výraz dosadíme za neznámou z do druhé rovnice. Získanou rovnici s neznámou y vyřešíme. Hodnotu neznámé y dosadíme do vyjádření neznámé z a vypočítáme její hodnotu.

Kdy rovnice nemá řešení

Soustava lineárních rovnic nemá žádné řešení tehdy, když jsou grafy jednotlivých rovnic navzájem rovnoběžné. Nekonečně mnoho řešení. Soustava lineárních rovnic má nekonečně mnoho řešení tehdy, když grafy jednotlivých rovnic tvoří tu samou přímku.

Co jsou to soustavy rovnic

Soustava rovnic představuje více rovnic, které řešíme dohromady. V soustavě se obvykle nachází více než jedna proměnná a řešením je tedy taková kombinace čísel, při jejichž dosazení za všechny proměnné mají rovnice smysl. Může se tak stát, že soustava rovnic má více než jedno řešení.

Co znamená kdyz v rovnici vyjde 0 0

Jesliže při úpravě jedné rovnice (lineární) vyjde rovnost dvou čísel (neznámá vypadne), např. 0 = 0, pak má nekonečně mnoho řešení. Vyjde-li nerovnost, např. 1 ≠ 3, rovnice nemá řešení.

Jak se zbavit zlomků v rovnici

Jsou-li v rovnici zlomky, odstraníme je násobením obou stran rovnice společným jmenovatelem zlomků.

Jak vyřešit rovnici o 3 neznámých

Soustava tří lineárních rovnic o třech neznámých má jedno, žádné nebo nekonečně mnoho řešení. Z libovolné rovnice vyjádříme jednu neznámou. Získaný výraz dosadíme za tuto neznámou do zbývajících dvou rovnic. Dvě nově vzniklé rovnice o dvou neznámých tvoří soustavu.

Jak se počítají nerovnice

Lineární nerovnice se řeší podobnými úpravami jako když počítáte běžnou lineární rovnici. Lineární nerovnice má zpravidla takovýto tvar: ax + b>0 (případně menší než, větší nebo rovno a menší nebo rovno). Nyní už stačí pouze upravit nerovnici do následující tvaru a výsledek je na světě: x>−b/a.

Kdy a jak používáme cramerovo pravidlo

Cramerovo pravidlo lze použít k důkazu, že problém celočíselného programování, jehož matice omezení je totálně unimodulární a jehož pravá strana je celočíselná, má celočíselná bázická řešení, což výrazně usnadňuje řešení úlohy.

Co znamená 0x 0

2. 0x = 0 Za x můžeme dosadit cokoli a vždy vyjde 0. 3. 0x = 5 Ať dosadíme za x jakékoli číslo, nikdy nemůže vyjít 5.

Kdy matice nemá řešení

Konkrétně podle Frobeniovy věty jakákoli soustava lineárních rovnic je nekonzistentní (nemá žádné řešení), pokud hodnost rozšířené matice je větší než hodnost matice koeficientů; pokud naopak řády těchto dvou matic jsou si rovny, soustava má alespoň jedno řešení.

Co znamená kdyz rovnice nemá řešení

Žádné řešení.

Soustava lineárních rovnic nemá žádné řešení tehdy, když jsou grafy jednotlivých rovnic navzájem rovnoběžné.

Jak se dělá zkouska u rovnic se zlomky

Zkoušku provádíme tak, že za neznámou dosadíme do obou stran rovnice vypočítaný kořen. V takovémto případě se snažíme zlomek (zlomky) odstranit pomoci ekvivalentní úpravy – vynásobit obě strany rovnice stejným nenulovým číslem – v našem případě číslem 3.

Jak se počítá se zlomky

Zlomek je jinak zapsaná operace dělení. Hodnotu zlomku vypočteme tak, že vydělíme čitatel jmenovatelem. Existuje i složený zlomek, což není nic jiného, než zlomek, který má v čitateli či jmenovateli další zlomek. Všechny tři zlomky mají stejnou hodnotu.

Jak se násobí zlomek

Při násobení zlomků tedy prostě vynásobíme čitatele prvního zlomku a čitatele druhého zlomku a dostaneme výsledný čitatel, podobně pro jmenovatele: a b ⋅ c d = a ⋅ c b ⋅ d \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d} ba⋅dc=b⋅da⋅c.

Kdy se mění znaménko nerovnosti

Postup řešení nerovnic je obdobný, jako při řešení rovnic s tou výjimkou, že pokud násobíme nebo dělíme nerovnici záporným číslem, mění se znak nerovnosti v opačný.

Jak se zbavit absolutní hodnoty

Pokud je výraz pod absolutní hodnotou vždy kladný, pak můžeme absolutní hodnotu odstranit — je tam zbytečná. Pokud bereme x z intervalu (2, ∞), pak platí rovnost |x − 2| = x − 2 (tj. odstranili jsme absolutní hodnotu).

Jak se násobí matice

Pro součin matic musí být počet sloupců v první matici roven počtu řádků ve druhé matici. Výsledná matice má počet řádků první matice a počet sloupců druhé matice. (sloupcový vektor). Tento součin lze interpretovat jako aplikaci lineárního zobrazení reprezentovaného transformační maticí na vektor.

Jak se počítá nerovnice

Lineární nerovnice se řeší podobnými úpravami jako když počítáte běžnou lineární rovnici. Lineární nerovnice má zpravidla takovýto tvar: ax + b>0 (případně menší než, větší nebo rovno a menší nebo rovno). Nyní už stačí pouze upravit nerovnici do následující tvaru a výsledek je na světě: x>−b/a.

Co je triviální řešení

Homogenní soustava má tedy vždy řešení – tzv. „triviální řešení , které spočívá v tom, že za všechny neznámé dosadíme nuly (triviálním řešením je tedy uspořádaná n−tice tvořená samými nulami, též můžeme říci nulový vektor).

Jak se počítá inverzní matice

Výpočet inverzní matice pomocí řádkových úpravVedle sebe napíšeme matici, kterou chceme invertovat, a jednotkovou matici.Matici upravujeme na jednotkovou matici standardními způsoby:Každý úkon prováděný na upravované matici musíme provést i na jednotkové matici.Zkoušku provedeme vynásobením matice s její inverzí.