Kas ir RSA kriptogrāfija? Pilnīgs šī šifrēšanas algoritma ceļvedis

Kriptogrāfija ir izmantota civilizācijās dažādos formātos tūkstošiem gadu. Sākot no senajiem ēģiptiešiem līdz mūsdienu internetam, kriptogrāfijas izmantošana ziņojumu šifrēšanai un atšifrēšanai ir būtisks saziņas rīks.
RSA kriptogrāfija (precīzāk – RSA algoritms) ir visuresošākais asimetriskās šifrēšanas algoritms pasaulē. Tas, ko nodrošina vairāki kriptogrāfiski un matemātiski sasniegumi, ikviens, kurš lieto internetu, kādā vai citā veidā izmanto RSA kriptogrāfiju.

Lielākajā daļā kriptovalūtu tiek izmantots līdzīgs asimetriskas šifrēšanas veids kā RSA, kas pazīstams kā elipses līknes kriptogrāfija. Lai gan tie atšķiras, tie abi ir balstīti uz līdzīgiem jēdzieniem, un RSA izpratne ir svarīga, lai veicinātu izpratni par kriptogrāfijas valūtu tīklos izmantoto kriptogrāfiju.
Kriptogrāfiskais fons un simetriskā vs asimetriskā kriptogrāfija
Līdz 1970. gadiem kriptogrāfija galvenokārt balstījās uz simetrisku atslēgu izmantošanu. Simetrisko atslēgu algoritmos divi lietotāji, kas vēlas sazināties ar ziņojumu, izmanto vienādas kriptogrāfiskās atslēgas gan teksta šifrēšanai, gan šifrētā teksta atšifrēšanai. Atslēgas attēlo kopīgu noslēpumu starp abām pusēm, un tos var izmantot kā privātu saziņas veidu. Tomēr šim dizainam ir dažas raksturīgas problēmas, kas rada nopietnus tā izmantošanas trūkumus.
Piemēram, abām pusēm jāzina slepenā atslēga, lai šifrētu un atšifrētu ziņojumu. Ārpus personīgas tikšanās, lai apmainītos ar šo informāciju, ir nepieciešams ievērojams daudzums komunikācijas, lai to paveiktu privāti, izmantojot nesaistītus nesējus. Trešās puses, kas skatās šos kanālus, var iegūt slepeno atslēgu, un tādējādi tiek apdraudēta šifrēšanas metode. Turklāt simetriskas atslēgas šifrēšanas jēdziens nav mērogojams. Ja vēlaties nosūtīt šifrētus ziņojumus vairākiem cilvēkiem, jums jāiegaumē slepenā atslēga katrai no šīm saziņas līnijām. Acīmredzot tas ātri kļūst neērti un acīmredzami nav labākais modelis, ko izmantot kriptovalūtas tīklos, kur tiek apmainīta vērtība.
Risinājums tam bija tā dēvētā asimetriskā šifrēšana vai tautā vairāk dēvēta publiskās atslēgas kriptogrāfija. Asimetriskā šifrēšana izmanto divas atslēgas, publisko atslēgu un privāto atslēgu. Šī modeļa vienkāršākajā formā lietotājs var publicēt publisko atslēgu, ar kuru jebkurš cits var izmantot, lai nosūtītu šai personai šifrētu ziņojumu, un tikai persona, kas publicēja publisko atslēgu un kurai ir atbilstošā privātā atslēga, var atšifrēt un skatīt šo ziņojumu. Viena taustiņa izmantošana atceļ otra taustiņa izmantošanu, un atslēgas nav jāmaina pusēm, kuras vēlas sazināties.
Asimetrisko šifrēšanas modeli padarīja iespējami 2 izcili principi, kas radās Lielbritānijas matemātiķa Džeimsa Elisa 1970. gada sasnieguma rezultātā. Eliss aprakstīja ideju, ka šifrēšana un atšifrēšana ir savstarpējas apgrieztas darbības, pamatojoties uz 2 dažādām atslēgām..

Džeimss Eliss, attēls no Telegrāfs.
Jēdzienu parasti attēlo piekaramā atslēga un atslēga, piekaramā atslēga apzīmē publisko atslēgu un atslēga – privāto atslēgu. Lai praktiski izmantotu šo teoriju, attīstījās divi principi.
Trapdoor funkcija
Slazddurvja funkcija ir ļoti svarīgs jēdziens kriptogrāfijā, kur ir mazsvarīgi pāriet no viena stāvokļa uz citu, bet aprēķināt pretējā virzienā, atgriežoties sākotnējā stāvoklī, bez īpašas informācijas kļūst neiespējami, kas pazīstams kā “trapdoor”..
Tiek saukta mūsdienās pazīstamākā trapdoor funkcija, kas ir RSA kriptogrāfijas pamatā Galvenā faktorizācija. Būtībā galvenā faktorizācija (pazīstama arī kā Integer Factorization) ir skaitļu teorijas jēdziens, ka saliktos veselos skaitļus var sadalīt mazākos veselos skaitļos. Visi saliktie skaitļi (kas nav galvenie skaitļi), kas tiek sadalīti pēc to pamata, sastāv no galvenajiem skaitļiem. Šis process ir pazīstams kā galvenā faktorizācija, un tam ir nopietnas sekas, ja to piemēro kriptogrāfijai.
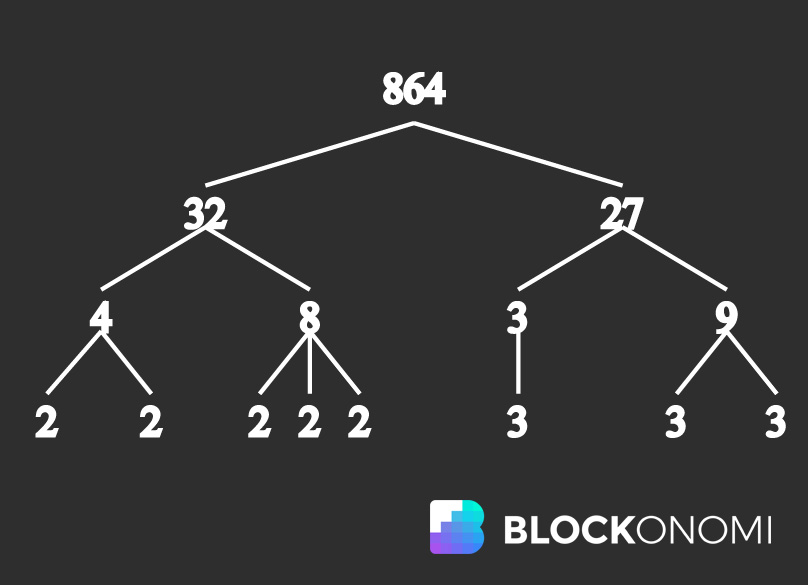
Prime Factorization, attēls izmantots no Vikipēdija
Būtībā ārkārtīgi lielu primāro skaitļu pamatfaktorizāciju nav iespējams aprēķināt, ņemot vērā milzīgo izmēģinājumu un kļūdu daudzumu, kas vajadzīgs, lai veiksmīgi aprēķinātu skaitli tā pamatelementos. Pašlaik nav efektīvu faktorizācijas algoritmu, lai to veiktu.
RSA un kā tā izmanto galveno faktorizāciju, ir aprakstīta nākamajā sadaļā, bet vispirms mums ir jāsaprot Diffie-Hellman Key Exchange.
Diffie-Hellman atslēgu birža
Diffie-Hellman atslēgu apmaiņa ir viens no pirmajiem publiskās atslēgas kriptogrāfijas protokoliem un principā ļauj droši un droši apmainīt kriptogrāfiskās atslēgas publiskā vidē. Vienkāršības labad mēģinājums konceptualizēt Diffie-Hellman Key Exchange un nākamā sadaļa par RSA algoritma darbību ir daudz mazsvarīgāka ar abstraktiem jēdzieniem, salīdzinot ar tīru matemātiku, tāpēc matemātiku izmantosim tikai tad, kad tas būs nepieciešams.
Visizplatītākais Diffie-Hellman Key Exchange konceptualizēšanas piemērs ir pazīstams kā Secret Color Exchange.
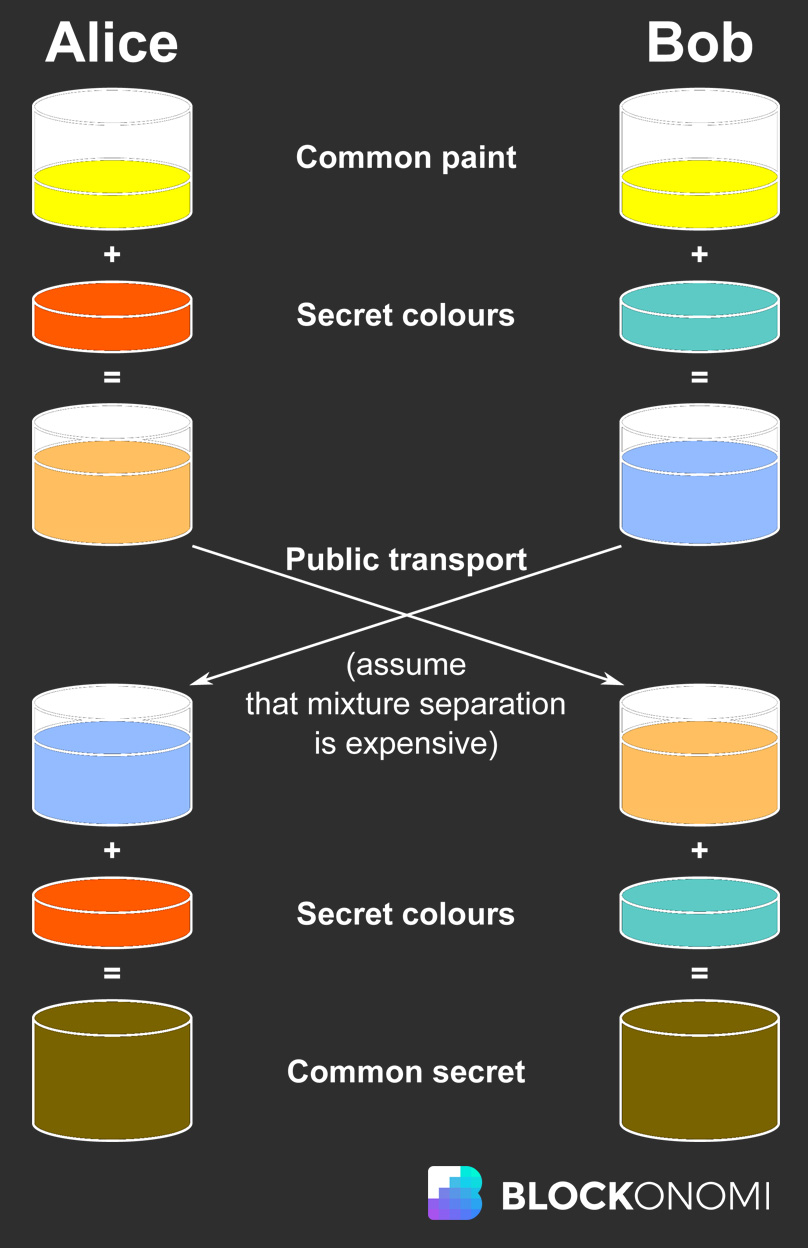
Diffie-Helman Key Exchange, attēls izmantots no Vikipēdija
Iepriekš redzamais attēls attēlo komunikācijas līniju starp Alisi un Bobu publiskā kanālā, kur Ieva var klausīties visu, kas tiek publiski paziņots starp Alisi un Bobu. Tātad, kā Alise un Bobs var sazināties ar privātu ziņojumu, izmantojot asimetrisku šifrēšanu, skaidri neapmainoties ar šo informāciju publiskajā vidē?
Viņi savā starpā apmainās ar slepenu informāciju, faktiski to nedalot. Process darbojas šādi:
1. solis
- Alise un Bobs ir vienisprātis, ka dzeltenā krāsa ir parasti izmantojamā krāsa. Šī informācija tiek pārraidīta pa publisko kanālu, lai arī Ieva to zinātu.
- Dzeltenais apzīmē publisko atslēgu.
- Alise slepeni nolemj, ka viņa kopā ar Dzelteno izmantos arī Zilo, un Bobs slepeni nolemj, ka viņš izmantos Sarkano ar Dzelteno.
- Alises izmantotais Zilais un Boba izmantotais sarkanais apzīmē viņu slepenās atslēgas.
2. solis
- Pēc tam gan Alise, gan Bobs savās slepenajās krāsās sajaucas ar dzeltenu, lai izveidotu saliktu krāsu.
- Alises maisījums rada Zaļo, bet Boba maisījums – apelsīnu.
- Tagad gan Alise, gan Bobs sūta viens otram savas saliktās krāsas.
- Arī Ieva saņem šīs krāsas, taču saskaras ar problēmu, šīs saliktās krāsas atspoguļo aizvērēja durvju funkciju.
- Divas krāsas ir viegli apvienot, lai izveidotu trešo krāsu, taču to nav iespējams mainīt. Ir ļoti grūti noteikt, kuras krāsas tika izmantotas, lai izveidotu trešo krāsu, tikai ar trešo krāsu un sākotnējo dzelteno krāsu.
3. solis
- Pēc tam Alise un Bobs sajaucas savās slepenajās krāsās ar saņemtajām saliktajām krāsām, kā rezultātā rodas šādi.
- Alise sajauc zilo ar Boba kompozītmateriālu apelsīnu.
- Bobs sajauc sarkano ar salikto zaļo no Alises.
- Abu maisījumu rezultātā rodas Brown.
Tas ir Diffie-Hellman Key Exchange noslēpums. Lai gan gan Alise, gan Bobs nonāca pie Brauna, viņi nekad nemainījās ar šo krāsu, un Ieva paliek bez nepieciešamās informācijas par slepenajām krāsām, lai varētu aprēķināt slepeno ziņojumu (Brauns).
Iepriekš minētais piemērs ir ļoti vienkārša vizualizācija, kā notiek apmaiņa. Izmantojot matemātiku, nodrošināto ziņojumu drošību un integritāti var panākt, izmantojot RSA kriptogrāfiju, kā aizturni izmantojot galveno faktorizāciju..
Kā darbojas RSA algoritms?
RSA algoritms darbojas, izmantojot asimetriskas šifrēšanas iespēju, izmantojot galveno faktorizācijas aizbīdni un Diffie-Hellman atslēgu apmaiņu. Būtībā RSA kriptogrāfija balstās uz primārās faktorizācijas grūtībām kā tās drošības metodi. Izmantojot ļoti vienkāršotu piemēru ar aprakstītu ierobežotu matemātiku, RSA algoritms satur 4 darbības.
- Atslēgu ģenerēšana – šīs darbības laikā lietotājs var izmantot nejaušu skaitļu ģeneratoru vai vienkārši izvēlēties 2 ļoti lielus primāros skaitļus (sauktus p un q). Šie skaitļi ir jāglabā slepenībā. Aprēķiniet n = pq, kur “n” ir gan publisko, gan privāto atslēgu modulis, un tā garumu sauc par atslēgas garumu. Padariet “n” publisku. Atslēgu izmēriem, kas ir vienādi vai lielāki par 1024 bitiem, nav efektīvas metodes, kā efektīvi atrisināt šo algoritmu (ļoti liela skaitļa “n” faktors). Pat lielākajam superdatoram pasaulē būtu nepieciešami tūkstošiem gadu, lai to atrisinātu. Tas ir pazīstams kā RSA problēma, un, ja tas tiks atrisināts, tas apdraudētu visas uz RSA balstītās kriptosistēmas.
- Atslēgu izplatīšana – Bobs vēlas nosūtīt Alisei slepenu informāciju, lai tiktu veiktas šādas darbības.
- Bobam ir jāzina Alises publiskā atslēga, lai šifrētu ziņojumu.
- Alisei ir jāzina sava privātā atslēga, lai atšifrētu ziņojumu.
- Lai Bobs varētu nosūtīt savu šifrēto ziņojumu, Alise nosūta Bobam savu publisko atslēgu.
- Alise nekad neizplata savu privāto atslēgu.
Var atrast padziļinātu RSA izmantoto matemātisko darbību skaidrojumu šeit, bet ir ārpus šī raksta darbības jomas.
Turklāt RSA šifrēšana ļauj digitāli parakstīt ziņojumus, kas ir vissvarīgākais kriptovalūtām un ir Bitcoin UTXO darījumu modeļa galvenā sastāvdaļa. Alise var digitāli parakstīt ziņojumu Bobam, lai pārbaudītu, vai viņš to ir nosūtījis (apstiprinot, ka tika izmantota viņas privātā atslēga), izveidojot ziņa jaukšanas vērtību un pievienojot to ziņai. Šo vērtību var pārbaudīt Bobs, kurš kopā ar Alises publisko atslēgu izmanto to pašu jaukšanas algoritmu un salīdzina iegūto jaukšanas vērtību ar ziņojuma faktisko jaukšanas vērtību..
Secinājums
RSA šifrēšana ir pasaulē visplašāk izmantotā asimetriskā šifrēšanas metode, jo tā spēj nodrošināt augstu šifrēšanas līmeni bez zināmiem algoritmiem, kas vēl varētu to atrisināt. Pamatojoties uz dažiem izciliem kriptogrāfijas un matemātikas sasniegumiem, tostarp Diffie-Hellman Key Exchange un trapdoor funkciju, RSA šifrēšana ir kļuvusi par vissvarīgāko, lai nodrošinātu drošu komunikāciju visā pasaulē..



